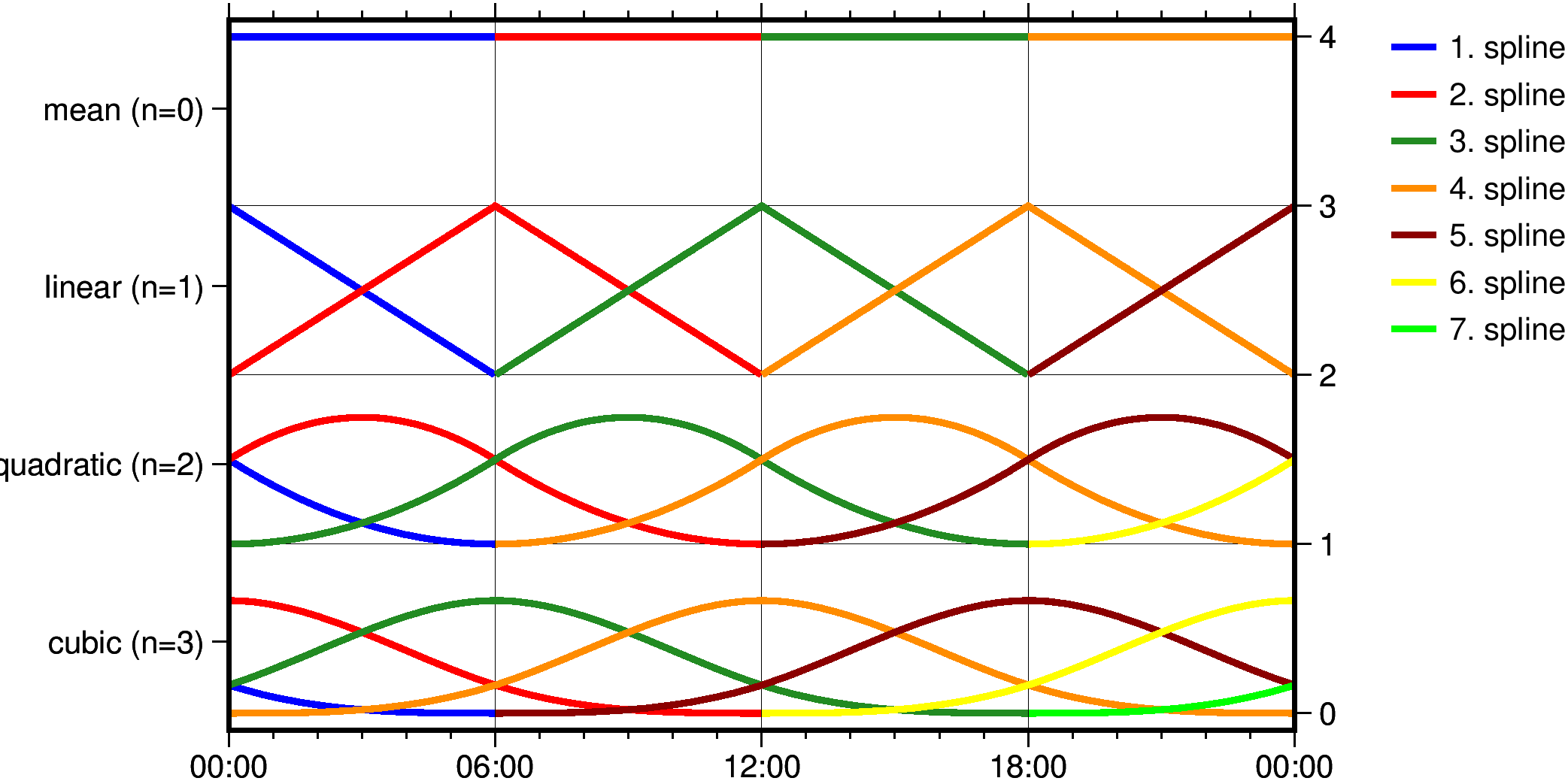
Basis splines
A time variable function is given by \[ f(x,t) = \sum_i f_i(x)\Psi_i(t), \]with the (spatial) coefficients $f_i(x)$ as parameters and the temporal basis functions $\Psi_i(t)$. Basis splines are defined as polynomials of degree $n$ in intervals between nodal points in time $t_i$:
- Block mean values ($n=0$) \[ \Psi_i(t) = \begin{cases} 1 & \text{if } t\in[t_i,t_{i+1}), \\ 0 & \text{otherwise} \end{cases} \]
- Linear splines ($n=1$) \[ \Phi_i(t) = \begin{cases} \tau_{i-1} & \text{if } t_{i-1}\le t \le t_i, \\ 1-\tau_i & \text{if } t_{i}\le t \le t_{i+1}, \\ 0 & \text{otherwise}. \end{cases} \]
- Quadratic splines ($n=2$) \[ \Phi_i(t) = \begin{cases} \frac{1}{2}\tau^2_{i-1} & \text{if } t_{i-1}\le t \le t_i, \\ -\tau^2_{i-1}+\tau_{i-1}+\frac{1}{2} & \text{if } t_{i}\le t \le t_{i+1}, \\ \frac{1}{2}\tau^2_{i-1}-\tau_{i-1}+\frac{1}{2} & \text{if } t_{i}\le t \le t_{i+1}, \\ 0 & \text{otherwise}. \end{cases} \]
- Cubic splines ($n=3$) \[ \Phi_i(t) = \begin{cases} \frac{1}{6}\tau^3 & \text{if } t_{i-1}\le t \le t_i, \\ -\frac{3}{6}\tau^3 +\frac{3}{6}\tau^2 +\frac{3}{6}\tau +\frac{1}{6} & \text{if } t_{i-1}\le t \le t_i, \\ \frac{3}{6}\tau^3 - \tau^2 +\frac{4}{6} & \text{if } t_{i-1}\le t \le t_i, \\ -\frac{1}{6}\tau^3 +\frac{3}{6}\tau^2 -\frac{3}{6}\tau +\frac{1}{6} & \text{if } t_{i-1}\le t \le t_i, \\ 0 & \text{otherwise}. \end{cases} \]