NormalsBuildShortTimeStaticLongTime
This program sets up normal equations based on observation. Additionally short time and long time variations can be parametrized based on the static parameters in observation in an efficient way. The observation equations are divided into time intervals $i \in \{1, ..., N\}$ (e.g. daily) as defined in inputfileArcList.
With estimateLongTimeVariations additional temporal variations can be co-estimated for a subset of the parameters selected by parameterSelection. These parameters might be spherical harmonic coefficients with a limited maximum degree. The temporal variations are represented by base functions $\Phi_k(t_i)$ (e.g. trend and annual oscillation) given by parametrizationTemporal. The temporal base functions are evaluated at the mid time $t_i$ of each interval $i$, multiplicated with the design matrix $\M A_i$ of the selected parameters, and the design matrix is extended accordingly.
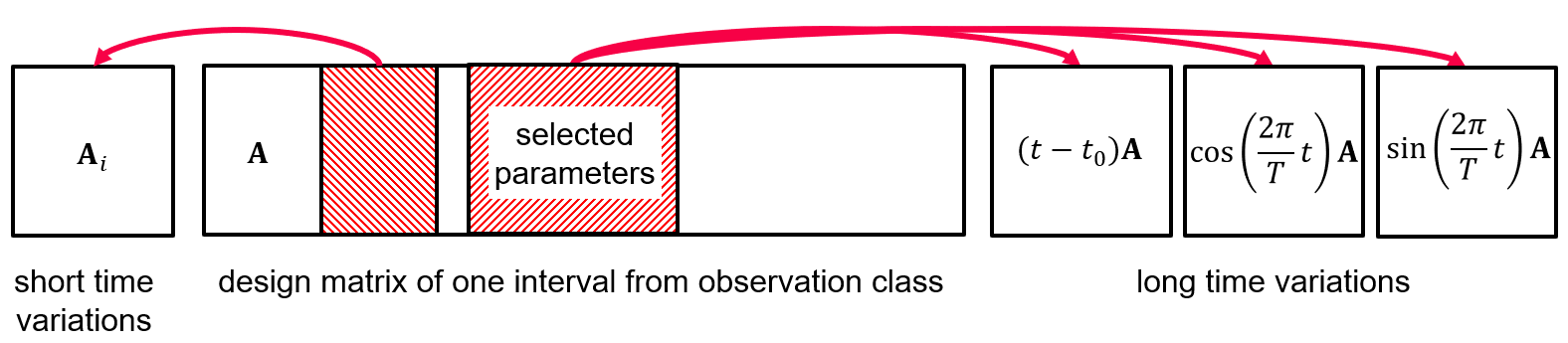
With estimateShortTimeVariations short time variations of the gravity field can be co-estimated. Their purpose is to mitigate temporal aliasing. The short time parameters selected by parameterSelection (e.g. daily constant or linear splines every 6 hour) are constrained by an autoregressiveModelSequence. If only a static parameter set is selected the coressponding part of the design matrix is copied and modeled as a constant value per interval in inputfileArcList additionally so the corresponding temporal factor can be expressed as \[ \Phi_i(t) = \begin{cases} 1 &\text{if} \hspace{5pt} t \in [t_i, t_{i+1}) \\ 0 & \text{otherwise} \end{cases}. \] Before writing the normal equations to outputfileNormalEquation short time gravity and satellite specific parameters can be eliminated with eliminateParameter.
Example: For the computation of the mean gravity field ITSG-Grace2018s with additional trend and annual signal the normal equations are computed month by month and accumulated afterwards (see NormalsAccumulate). The observations were divided into daily intervals with inputfileArcList. The static gravity field has been parametrized as spherical harmonics up to degree $n=200$ in observation:parametrizationGravity. The trend and annual signals defined by estimateLongTimeVariations:parametrizationTemporal were estimated for selected parameters up to degree $n=120$. To mitigate temporal aliasing daily gravity fields up to degree $n=40$ were setup and constrained with an autoregressiveModelSequence up to order three.
A detailed description of the approach is given in: Kvas, A., Mayer-Gürr, T. GRACE gravity field recovery with background model uncertainties. J Geod 93, 2543–2552 (2019). https://doi.org/10.1007/s00190-019-01314-1.
| Name | Type | Annotation |
|---|---|---|
outputfileNormalEquation | filename | outputfile for normal equations |
observation | observation | |
estimateShortTimeVariations | sequence | co-estimate short time gravity field variations |
autoregressiveModelSequence | autoregressiveModelSequence | AR model sequence for constraining short time gravity variations |
parameterSelection | parameterSelector | parameters describing the short time gravity field |
estimateLongTimeVariations | sequence | co-estimate long time gravity field variations |
parametrizationTemporal | parametrizationTemporal | parametrization of time variations (trend, annual, ...) |
parameterSelection | parameterSelector | parameters describing the long time gravity field |
inputfileArcList | filename | list to correspond points of time to arc numbers |
defaultBlockSize | uint | block size for distributing the normal equations, 0: one block |
eliminateParameter | boolean | eliminate short time and state parameter |