ParametrizationGnssAntenna
Parametrization of antenna center variations. It will be used to set up the design matrix in a least squares adjustment. Usually the parametrization is setup separately for different gnssType.
If multiple parametrizations are given the parameters are sequently appended in the design matrix and parameter vector.
Center
Antenna center or, if setup for a specific gnssType,
phase/code center offset (e.g. *1*G for GPS L1 phase center offset) in $[m]$.
The parameter names are
*:antennaCenter.x:*:*,-
*:antennaCenter.y:*:*, -
*:antennaCenter.z:*:*.
| Name | Type | Annotation |
|---|---|---|
estimateX | boolean | |
estimateY | boolean | |
estimateZ | boolean |
SphericalHarmonics
Parametrization of antenna center variations in $[m]$ in terms of spherical harmonics. As usually only data above the horizon are observed only the even spherical harmonics (degree/order $m+n$ even), which are symmetric to the equator, are setup.
The total count of parameters is $((n_{max}+1)(n_{max}+2)-n_{min}(n_{min}+1)/2$ and the parameter names are
*:antennaCenterVariations.sphericalHarmonics.c_<degree>_<order>:*:*,-
*:antennaCenterVariations.sphericalHarmonics.s_<degree>_<order>:*:*.
| Name | Type | Annotation |
|---|---|---|
minDegree | uint | min degree |
maxDegree | uint | max degree |
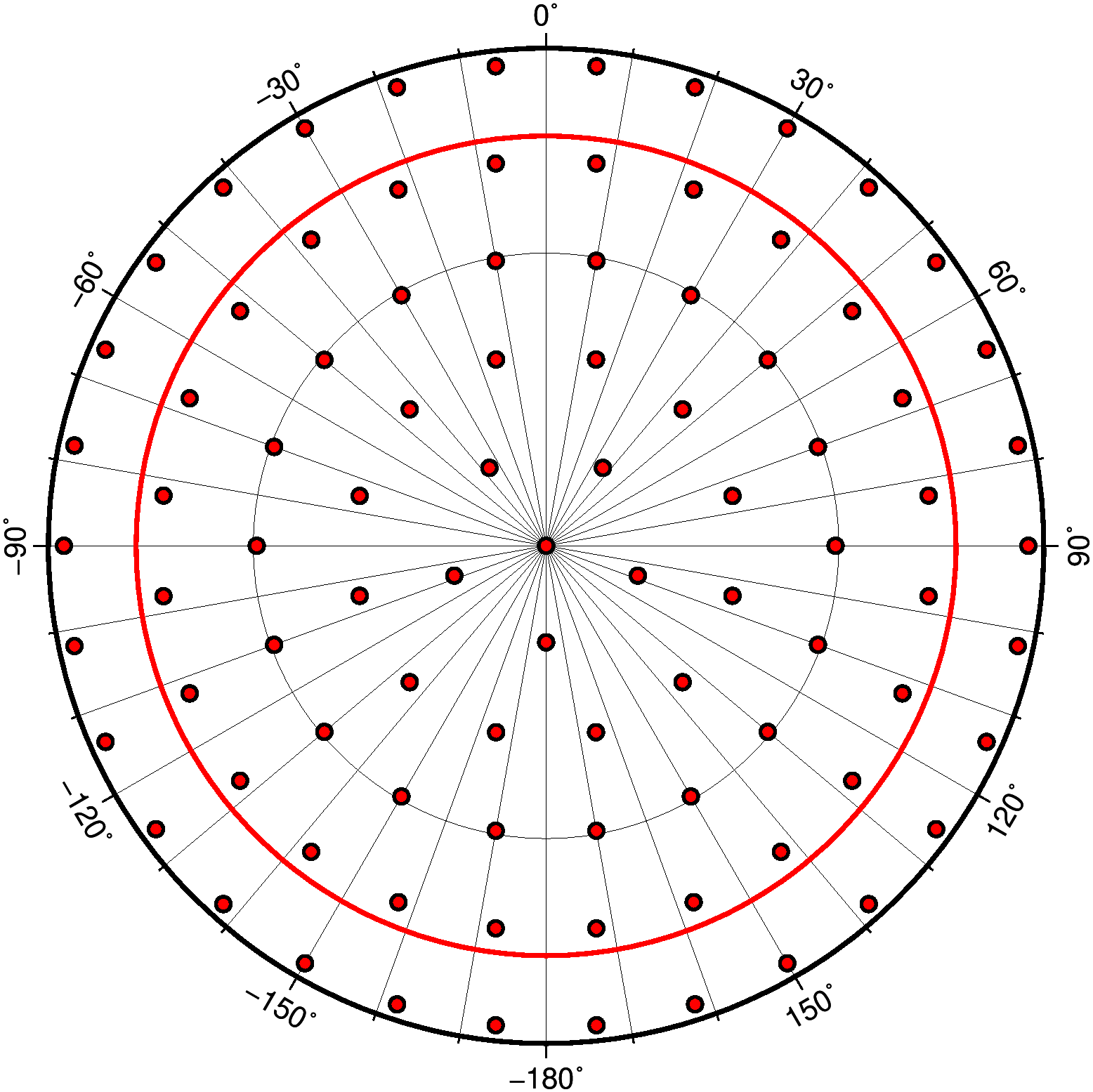
RadialBasis
Parametrization of antenna center variations with radial basis functions
\[
ACV(\M x(A, E)) = \sum_i a_i \Phi(\M x\cdot\M x_i)
\]where $a_i$ in $[m]$ the coefficients which has to be estimated and $\Phi$ are the basis
functions
\[
\Phi(\cos\psi) = \sum_n \sqrt{2n+1}P_n(\cos\psi).
\]
The parameter names are
*:antennaCenterVariations.radialBasis.<index>.<total count>:*:*.
| Name | Type | Annotation |
|---|---|---|
grid | grid | nodal points of shannon kernels |
minDegree | uint | min degree of shannon kernel |
maxDegree | uint | max degree of shannon kernel |