GnssProcessingStep
Processing step in GnssProcessing.
Processing steps enable a dynamic definition of the consecutive steps performed during any kind of GNSS processing. The most common steps are estimate, which performs an iterative least squares adjustment, and writeResults, which writes all output files defined in GnssProcessing and is usually the last step. Some steps such as selectParametrizations, selectEpochs, selectNormalsBlockStructure, and selectReceivers affect all subsequent steps. In case these steps are used within a group or forEachReceiverSeparately step, they only affect the steps within this level.
For usage examples see cookbooks on GNSS satellite orbit determination and network analysis or Kinematic orbit determination of LEO satellites.
Estimate
Iterative non-linear least squares adjustment. In every iteration it accumulates the system of normal equations, solves the system and updates the estimated parameters. The estimated parameters serve as a priori values in the next iteration and the following processing steps. Iterates until either every single parameter update (converted to an influence in meter) is below a convergenceThreshold or maxIterationCount is reached.
With computeResiduals the observation equations are computed again after each update to compute the observation residuals.
The overall standard deviation of a single observation used for the weighting is composed of several factors \[ \hat{\sigma}_i = \hat{\sigma}_i^{huber} \hat{\sigma}_{[\tau\nu a]}^{recv} \sigma_{[\tau\nu a]}^{recv}(E,A), \]where $[\tau\nu a]$ is the signal type, the azmiuth and elevation dependent $\sigma_{[\tau\nu a]}^{recv}(E,A)$ is given by receiver:inputfileAccuracyDefinition and the other factors are estimated iteratively from the residuals.
With computeWeights a standardized variance $\hat{s}_i^2$ for each residual $\hat{\epsilon}_i$ is computed \[ \hat{s}_i^2 = \frac{1}{\hat{\sigma}_{[\tau\nu a]}^{recv} \sigma_{[\tau\nu a]}^{recv}(E,A)}\frac{\hat{\epsilon}_i^2}{r_i} \qquad\text{with}\qquad r_i = \left(\M A\left(\M A^T\M A\right)^{-1}\M A^T\right)_{ii} \]taking the redundancy $r_i$ into account. If $\hat{s}_i$ is above a threshold huber the observation gets a higher standard deviation used for weighting according to \[ \hat{\sigma}_i^{huber} = \left\{ \begin{array}{ll} 1 & s < huber,\\ (\hat{s}_i/huber)^{huberPower} & s \ge huber \end{array} \right., \]similar to robust least squares adjustment.
With adjustSigma0 individual variance factors can be computed
for each station and all phases of a system and each code observation type
(e.g. for each L**G, L**E, C1CG, C2WG, C1CE, … )
separately
\[
\hat{\sigma}_{[\tau\nu a]}^{recv} = \sqrt{\frac{\hat{\M\epsilon}^T\M P\hat{\M\epsilon}}{r}}.
\]
| Name | Type | Annotation |
|---|---|---|
computeResiduals | boolean | |
adjustSigma0 | boolean | adjust sigma0 by scale factor (per receiver and type) |
computeWeights | boolean | downweight outliers |
huber | double | residuals > huber*sigma0 are downweighted |
huberPower | double | residuals > huber: sigma=(e/huber)^huberPower*sigma0 |
convergenceThreshold | double | [m] stop iteration once full convergence is reached |
maxIterationCount | uint | maximum number of iterations |
ResolveAmbiguities
Performs a least squares adjustment like processingStep:estimate but with additional integer phase ambiguity resolution. After this step all resolved ambiguities are removed from the normal equation system. Only ambiguites are resolved with involved selectTransmitters/Receivers.
Integer ambiguity resolution is performed based on the least squares ambiguity decorrelation adjustment (LAMBDA) method (Teunissen 1995, DOI 10.1007/BF00863419), specifically the modified algorithm (MLAMBDA) by Chang et al. (2005, DOI 10.1007/s00190-005-0004-x). First the covariance matrix of the integer ambiguity parameters is computed by eliminating all but those parameters from the full normal equation matrix and inverting it. Then, a Z-transformation is performed as described by Chang et al. (2005) to decorrelate the ambiguity parameters without losing their integer nature.
The search process follows MLAMBDA and uses integer minimization of the weighted sum of squared residuals.
It is computationally infeasible to search a hyper-ellipsoid with a dimension of ten thousand or more.
Instead, a blocked search algorithm is performed by moving a window with a length of, for example,
searchBlockSize=200 parameters over the decorrelated ambiguities, starting from the most accurate.
In each step, the window is moved by half of its length and the overlapping parts are compared to each other.
If all fixed ambiguities in the overlap agree, the algorithm continues.
Otherwise, both windows are combined and the search is repeated using the combined window, again comparing with the overlapping
part of the preceding window. If not all solutions could be checked for a block after maxSearchSteps,
the selected incompleteAction is performed.
If the algorithm reaches ambiguities with a standard deviation higher than sigmaMaxResolve,
ambiguity resolution stops and the remaining ambiguities are left as float values.
Otherwise, all ambiguity parameters are fixed to integer values.
In contrast to an integer least squares solution over the full ambiguity vector, it is not guaranteed that the resulting solution is optimal in the sense of minimal variance with given covariance. This trade-off is necessary to cope with large numbers of ambiguities.
| Name | Type | Annotation |
|---|---|---|
outputfileAmbiguities | filename | resolved ambiguities |
selectTransmitters | platformSelector | only resolve ambiguities with these participating transmitters |
selectReceivers | platformSelector | only resolve ambiguities with these participating receivers |
sigmaMaxResolve | double | max. allowed std. dev. of ambiguity to resolve [cycles] |
searchBlockSize | uint | block size for blocked integer search |
maxSearchSteps | uint | max. steps of integer search for each block |
incompleteAction | choice | if not all solutions tested after maxSearchSteps |
stop | stop searching, ambiguities remain float in this block | |
resolve | use best integer solution found so far | |
shrinkBlockSize | try again with half block size | |
throwException | stop and throw an exception | |
computeResiduals | boolean | |
adjustSigma0 | boolean | adjust sigma0 by scale factor (per receiver and type) |
computeWeights | boolean | downweight outliers |
huber | double | residuals > huber*sigma0 are downweighted |
huberPower | double | residuals > huber: sigma=(e/huber)^huberPower*sigma0 |
ComputeCovarianceMatrix
Accumulates the normal equations and computes the covariance matrix as inverse of the normal matrix. It is not the full inverse but only the elements which are set in the normal matrix (see gnssProcessingStep:selectNormalsBlockStructure) are computed. The matrix is passed to the parametrizations. Only used in parametrizations:kinematicPositions to get the epoch wise covariance information at the moment.
WriteResults
In this step all outputfiles defined in parametrizations are written. It considers the settings of processingStep:selectParametrizations, processingStep:selectEpochs, and processingStep:selectReceivers.
It is usually the last processing step, but can also be used at other points in the processing in combination with suffix to write intermediate results, for example before gnssProcessingStep:resolveAmbiguities to output the float solution.
| Name | Type | Annotation |
|---|---|---|
suffix | string | appended to every output file name (e.g. orbit.G01.suffix.dat) |
WriteNormalEquations
Accumulates the normal equations matrix and writes it. If remainingParameters is set only the selected parameters are written to the normal equations and all other parameters are eliminated beforehand (implicitly solved).
The solution of the normals would results in $\Delta\M x$ (see parametrizations). To write the appropriate apriori vector $\M x_0$ use processingStep:writeAprioriSolution.
| Name | Type | Annotation |
|---|---|---|
outputfileNormalEquations | filename | normals |
remainingParameters | parameterSelector | parameter order/selection of output normal equations |
constraintsOnly | boolean | write only normals of constraints without observations |
defaultNormalsBlockSize | uint | block size for distributing the normal equations, 0: one block, empty: original block size |
WriteAprioriSolution
Writes the current apriori vector $\M x_0$ (see parametrizations). If remainingParameters is set only the selected parameters are written.
| Name | Type | Annotation |
|---|---|---|
outputfileAprioriSolution | filename | a priori parameters |
outputfileParameterNames | filename | parameter names |
remainingParameters | parameterSelector | parameter order/selection of output normal equations |
WriteResiduals
Writes the observation residuals for all
selectReceivers.
For for each station a file is written. The file name is interpreted as
a template with the variable {station} being replaced by the station name.
| Name | Type | Annotation |
|---|---|---|
selectReceivers | platformSelector | subset of used stations |
outputfileResiduals | filename | variable {station} available |
WriteUsedStationList
Writes a list of receivers (stations) which are used in the last step and selected by selectReceivers.
| Name | Type | Annotation |
|---|---|---|
selectReceivers | platformSelector | subset of used stations |
outputfileUsedStationList | filename | ascii file with names of used stations |
WriteUsedTransmitterList
Writes a list of transmitters which are used in the last step and selected by selectTransmitters.
| Name | Type | Annotation |
|---|---|---|
selectTransmitters | platformSelector | subset of used transmitters |
outputfileUsedTransmitterList | filename | ascii file with PRNs |
PrintResidualStatistics
Print residual statistics.
areq: C1CG**: factor = 0.64, sigma0 = 1.00, count = 2748, outliers = 48 (1.75 %) areq: C1WG**: factor = 0.50, sigma0 = 1.00, count = 2748, outliers = 43 (1.56 %) areq: C2WG**: factor = 0.50, sigma0 = 1.00, count = 2748, outliers = 59 (2.15 %) areq: C5XG**: factor = 0.46, sigma0 = 1.00, count = 1279, outliers = 23 (1.80 %) areq: L1CG**: factor = 0.86, sigma0 = 0.96, count = 2748, outliers = 40 (1.46 %) areq: L1WG**: factor = 0.86, sigma0 = 1.02, count = 2748, outliers = 40 (1.46 %) areq: L2WG**: factor = 0.86, sigma0 = 0.96, count = 2748, outliers = 40 (1.46 %) areq: L5XG**: factor = 0.86, sigma0 = 1.30, count = 1279, outliers = 14 (1.09 %) areq: C1PR**: factor = 0.48, sigma0 = 1.00, count = 1713, outliers = 53 (3.09 %) areq: C2PR**: factor = 0.55, sigma0 = 1.00, count = 1713, outliers = 51 (2.98 %) areq: L1PR**: factor = 0.85, sigma0 = 1.09, count = 1713, outliers = 29 (1.69 %) areq: L2PR**: factor = 0.85, sigma0 = 0.88, count = 1713, outliers = 29 (1.69 %) areq: C1XE**: factor = 0.44, sigma0 = 1.00, count = 1264, outliers = 21 (1.66 %) areq: C5XE**: factor = 0.33, sigma0 = 1.00, count = 1264, outliers = 27 (2.14 %) areq: C7XE**: factor = 0.28, sigma0 = 1.00, count = 1264, outliers = 41 (3.24 %) areq: L1XE**: factor = 0.82, sigma0 = 1.14, count = 1264, outliers = 15 (1.19 %) areq: L5XE**: factor = 0.82, sigma0 = 0.84, count = 1264, outliers = 15 (1.19 %) areq: L7XE**: factor = 0.82, sigma0 = 0.94, count = 1264, outliers = 15 (1.19 %) badg: C1CG**: factor = 1.25, sigma0 = 1.00, count = 2564, outliers = 47 (1.83 %) ...
SelectParametrizations
Enable/disable parameter groups and constraint groups for subsequent steps, e.g. processingStep:estimate or processingStep:writeResults. The name and nameConstraint of these groups are defined in parametrizations. Prior models or previously estimated parameters used as new apriori $\M x_0$ values are unaffected and they are always reduced from the observations. This means all unselected parameters are kept fixed to their last result.
An example would be to process at a 5-minute sampling using
processingStep:selectEpochs
and then at the end to densify the clock parameters to the full 30-second observation sampling
while keeping all other parameters fixed
(disable=*, enable=*.clock*, enable=parameter.STEC).
| Name | Type | Annotation |
|---|---|---|
parametrization | choice | |
enable | sequence | |
name | string | wildcards: * and ? |
disable | sequence | |
name | string | wildcards: * and ? |
SelectEpochs
Select epochs for subsequent steps. This step can be used to reduce the processing sampling
while keeping the original observation sampling for all preprocessing steps (e.g. outlier and cycle slip detection).
Another example is to process at a 5-minute sampling by setting nthEpoch=10 and then
at the end to densify only the clock parameters to the full 30-second observation sampling by
setting nthEpoch=1 while keeping all other parameters fixed
with processingStep:selectParametrizations.
| Name | Type | Annotation |
|---|---|---|
nthEpoch | uint | use only every nth epoch in all subsequent processing steps |
SelectNormalsBlockStructure
Select block structure of sparse normal equations for subsequent steps.
This step can be used to define the structure of the different parts of the normal equation system, which can have a major impact on computing performance and memory consumption depending on the processing setup.
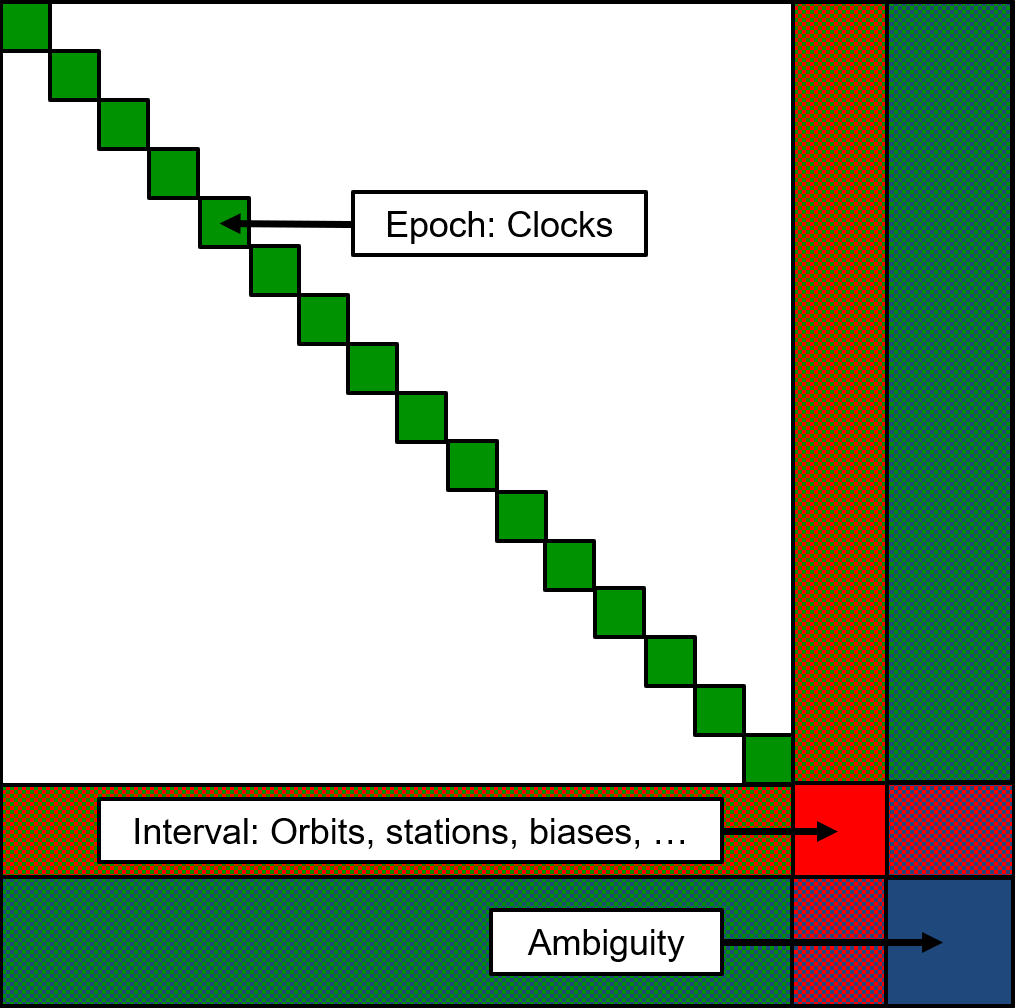
The normal equation system is divided into three parts for epoch, interval, and ambiguity parameters. The epoch part is subdivided further into one subpart per epoch. Each part is divided into blocks and only non-zero blocks are stored in memory to reduce memory consumption and to prevent unnecessary matrix computations. defaultBlockSizeEpoch, defaultBlockSizeInterval, and defaultBlockSizeAmbiguity control the size of the blocks within each part of the normal equations. defaultBlockReceiverCount can be set to group a number of receivers into one block within the epoch and interval parts.
If keepEpochNormalsInMemory=no epoch blocks are eliminated after they are set up to reduce the number
of parameters in the normal equation system. defaultBlockCountReduction controls after how many epoch blocks
an elimination step is performed. For larger processing setups or high sampling rates epoch block elimination is recommended
as the large number of clock parameters require a lot of memory.
| Name | Type | Annotation |
|---|---|---|
defaultBlockSizeEpoch | uint | block size of epoch parameters, 0: one block |
defaultBlockSizeInterval | uint | block size of interval parameters, 0: one block |
defaultBlockSizeAmbiguity | uint | block size of ambiguity parameters, 0: one block |
defaultBlockReceiverCount | uint | number of receivers to group into one block for epoch and interval |
defaultBlockCountReduction | uint | minimum number of blocks for epoch reduction |
keepEpochNormalsInMemory | boolean | speeds up processing but uses much more memory |
accumulateEpochObservations | boolean | set up all observations per epoch and receiver at once |
SelectReceivers
This step can be used to process only a subset of stations in subsequent processing steps. The most common use is to start the processing with a well-distributed network of core stations as seen in GNSS satellite orbit determination and network analysis. To later process all other stations individually, use the processing step processingStep:forEachReceiverSeparately and select all stations excluding the core stations in that step.
| Name | Type | Annotation |
|---|---|---|
selectReceivers | platformSelector |
ForEachReceiverSeparately
Perform these processing steps for each selectReceivers separately. All non-receiver related parameters parameters are disabled in these processing steps (see .
This step can be used for individual precise point positioning (PPP) of all stations. During GNSS satellite orbit determination and network analysis this step is used after the initial processing of the core network to process all other stations individually. In that case provide the same station list as inputfileExcludeStationList in this step that was used as inputfileStationList in the selectReceivers step where the core network was selected.
| Name | Type | Annotation |
|---|---|---|
selectReceivers | platformSelector | |
variableReceiver | string | variable is set for each receiver |
processingStep | gnssProcessingStep | steps are processed consecutively |
Group
Perform these processing steps. This step can be used to structure complex processing flows. The select.. processing steps defined within a group only affect the steps within this group.
| Name | Type | Annotation |
|---|---|---|
processingStep | gnssProcessingStep | steps are processed consecutively |
DisableTransmitterShadowEpochs
Disable transmitter epochs during eclipse. With proper attitude modeling (see SimulateStarCameraGnss) this is usually not necessary.
| Name | Type | Annotation |
|---|---|---|
selectTransmitters | platformSelector | |
disableShadowEpochs | boolean | disable epochs if satellite is in Earth's/Moon's shadow |
disablePostShadowRecoveryEpochs | boolean | disable epochs if satellite is in post-shadow recovery maneuver for GPS block IIA |
ephemerides | ephemerides | |
eclipse | eclipse | eclipse model used to determine if a satellite is in Earth's shadow |