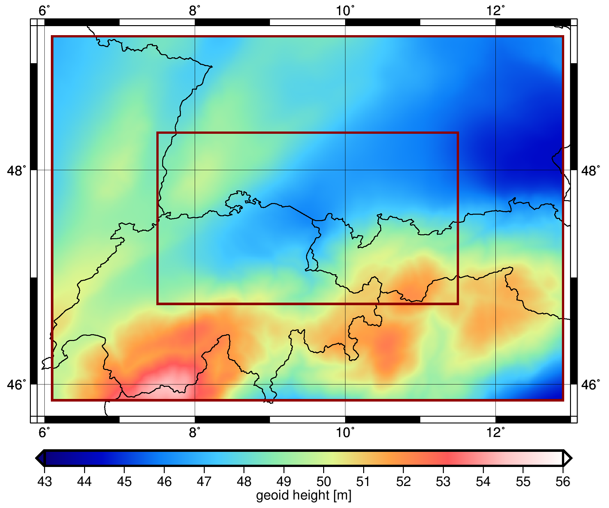
Regional geoid determination

This shows exemplary the computation of a regional geoid using terrestrial gravimetric observations in combination with a global satellite model such as GOCO06s. The geoid is estimated in a least squares adjustment with a parametrization using radial basis functions. A detailed desciption of the method is given in Christian Pock (2017), Consistent Combination of Satellite and Terrestrial Gravity Field Observations in Regional Geoid Modeling. Dissertation TU Graz.

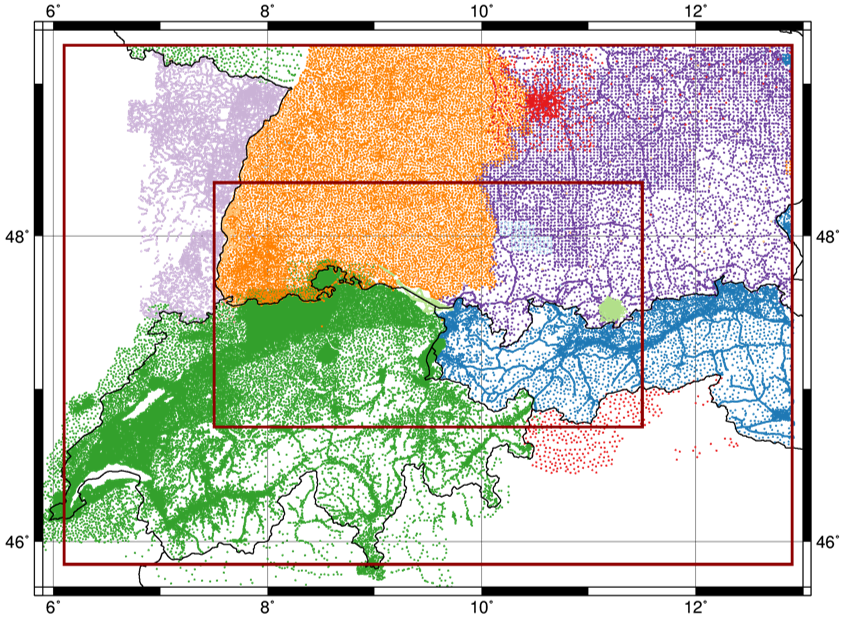
Gravimetric data

Here it is assumed that the measured absolute gravity data is given at points in ellipsoidal coordinates. The observed values should be converted to SI units $m/s^2$.

• Matrix2GriddedData to convert data from text file in tabular form.

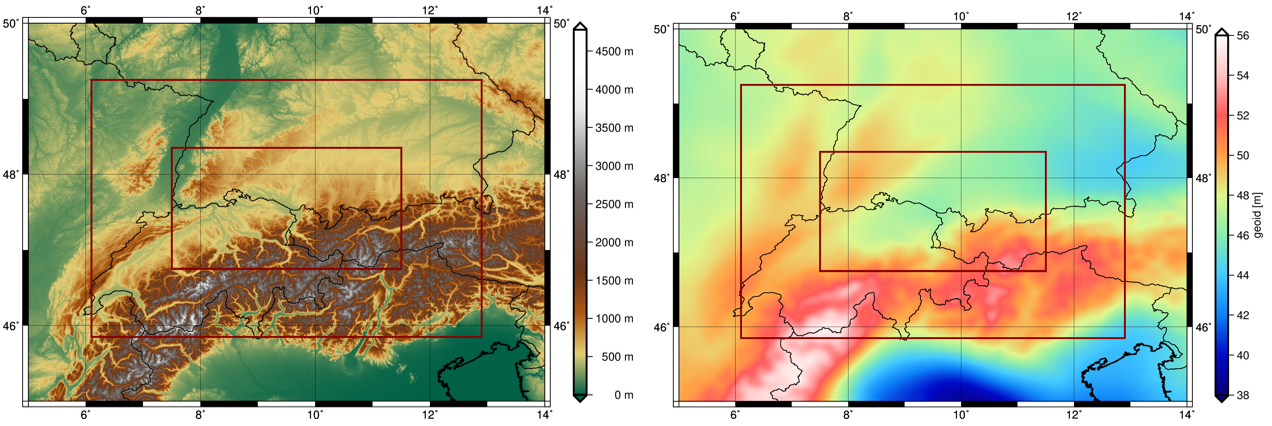
Topography

A high resolution topography model is needed to reduce the observations. As the model heights are usually given in physical heights a reference geoid is needed to compute the correct ellipsoidal height.

• NetCdf2GridRectangular convert into groops format.
• Gravityfield2GriddedData: Compute geoid heights using the GOCO06s model with
  • grid:file The topography grid
  • kernel:geoidHeight
  • gravityfield:potentialCoefficients the GOCO06s model
  • gravityfield:potentialCoefficients Subtract (factor=-1) GRS680 normal field.
• GriddedDataCalculate: Generate a new combined griddedData file with the orthometric height (data0) and the geoid height (data1).
• GriddedTopography2PotentialCoefficients: Compute the gravitational potential in terms of spherical harmonics up to a maximum degree of the global satellite model. This is the part of the topography, which is already included in the global satellite model. The integration boundaries are radialUpperBound=data0+data1 and radialLowerBound=data1.

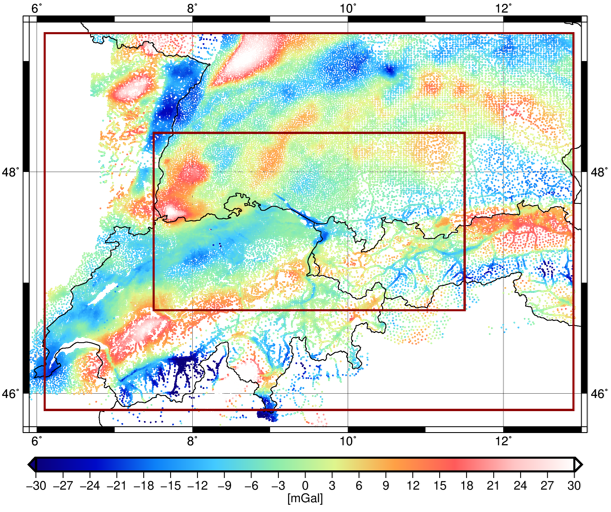
Reduce

Calculate approximate reference gravity to reduce it from the observations.

• Gravityfield2AbsoluteGravity
  • grid:File at observation positions
  • gravityfield:tides Centrifugal potential
  • gravityfield:potentialCoefficients full GOCO06s model
  • gravityfield:topography (radialUpperBound=data0+data1, radialLowerBound=data1)
  • gravityfield:potentialCoefficients Subtract (factor=-1) the potential part of the topography already included in the GOCO06s model.
• GriddedDataCalculate to calculate observed minus computed.
• Large outliers can be removed in GriddedDataCalculate with removalCriteria.

Radial Basis Functions (RBF)

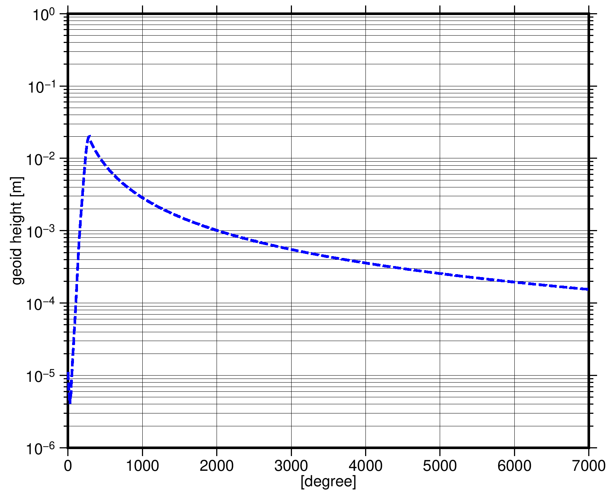
The residual gravity is parametrized in terms of Radial Basis Functions parametrizationGravity:radialBasis. The basis functions should be distributed on a regular grid covering a somewhat larger area than the observations, see border. The shape of the functions kernel:coefficients should reflect the signal content of reduced observations and are defined by the coefficients.

• RadialBasisSplines2KernelCoefficients
  • gravityfield:potentialCoefficients accuracies of GOCO06s model
  • maxDegree=7000. Complemented by Kaula's rule of thumb

The maximum degree should correspond to the spatial resolution. Rule of thumb: the number of spherical harmonic coefficients $(\text{maxDegree}+1)^2$ should roughly agree to the number of grid points if they would cover the complete Earth.

Compute: Estimate parameters in a least squares adjustment

Setup the observation equations and accumulate the system of normal equations.

• NormalsBuild
  • normalEquation:design with observation:terrestrial
    • kernel:disturbance
    • parametrizationGravity:radialBasis with kernel:coefficients
• NormalsSolverVCE
  • normalEquation:file from NormalsBuild
  • normalEquation:regularization towards zero means regularization towards the GOCO06s, which is reduced from the data.

Restore: Calculate the geoid solution

Evaluate the estimated parameters and add back the reduced reference models.

• Gravityfield2GriddedData: Compute approximate geoid heights using the GOCO06s model with
  • grid select a grid with target resolution at elliposid
  • kernel:geoidHeight
  • gravityfield:potentialCoefficients GOCO06s model
  • gravityfield:potentialCoefficients Subtract (factor=-1) GRS80 normal field.
• GriddedDataCalculate: Move points from ellipsoid to geoid with height=data0
• Gravityfield2GriddedData
  • grid:file from above.
  • kernel:geoidHeight
  • gravityfield:fromParametrization The solution vector $\M x$ together with the RBF parametrization
  • gravityfield:potentialCoefficients GOCO06s model
  • gravityfield:topography (radialUpperBound=data0+data1, radialLowerBound=data1)
  • gravityfield:potentialCoefficients Subtract (factor=-1) the potential part of the topography already included in the GOCO06s model.
  • gravityfield:potentialCoefficients Subtract (factor=-1) GRS80 normal field.
  • convertToHarmonics=no, otherwise the RBF are converted to harmonics up to degree 7000.
• GriddedDataCalculate: Set height=0 of the computed geoid grid.
• GridRectangular2NetCdf